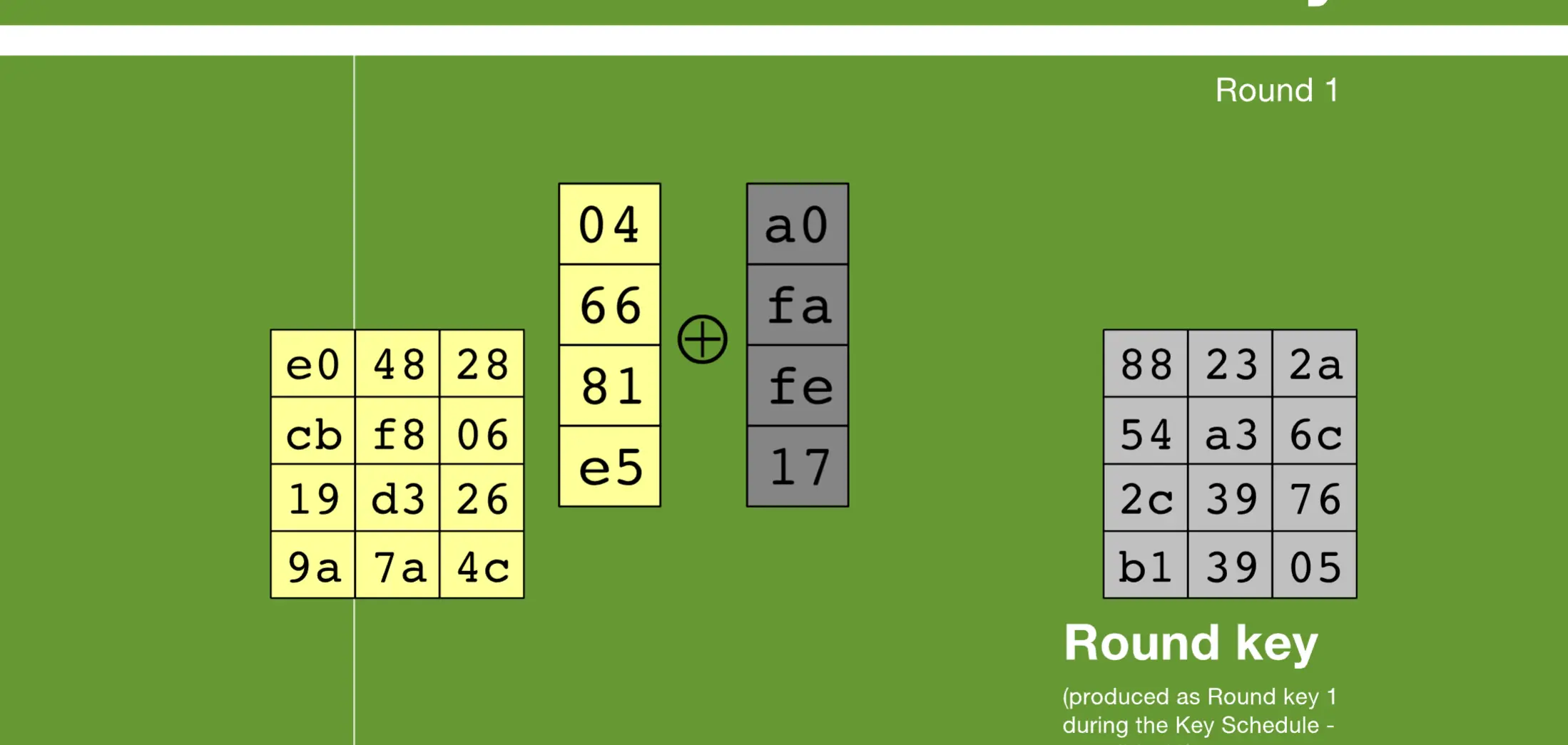
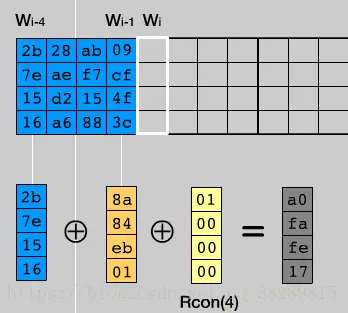
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
| import copy
def mul(poly1, poly2): # 两个多项式相乘
result = 0
for index in range(poly2.bit_length()):
if poly2 & (1 << index):
result ^= (poly1 << index)
return result
def mod(poly, mod = 0b100011011): # 多项式poly模多项式100011011
while poly.bit_length() > 8:
poly ^= (mod << (poly.bit_length() - 9))
return poly
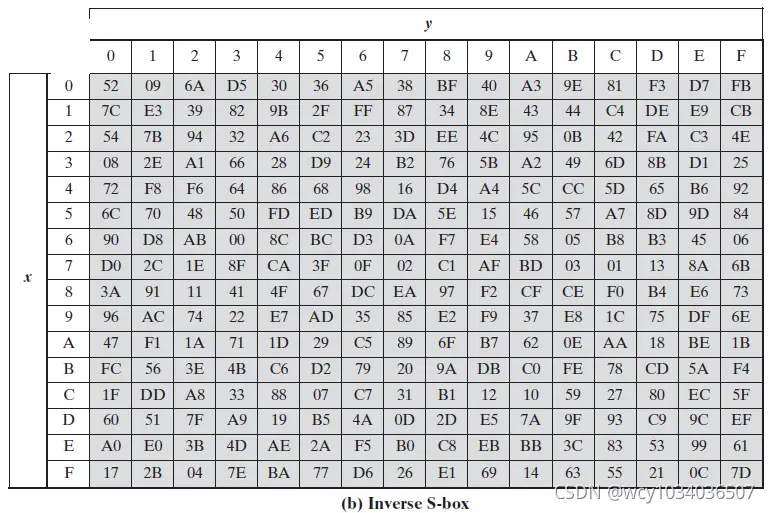
def substitute(m_hex, inverse=False):
m_s = []
box = s_box if not inverse else i_s_box
for i in m_hex:
x, y = int(i, 16) // 16, int(i, 16) % 16
temp = hex(box[x*16+y])
m_s.append(temp)
return m_s
s_box = [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]
i_s_box = [0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB, 0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB, 0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E, 0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25, 0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92, 0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84, 0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06, 0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B, 0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73, 0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E, 0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B, 0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4, 0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F, 0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF, 0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61, 0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D]
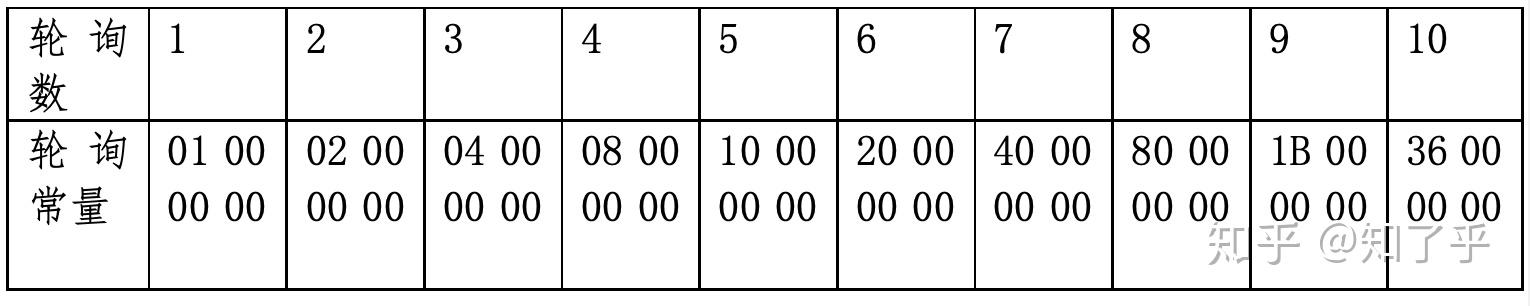
rcon = [0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]
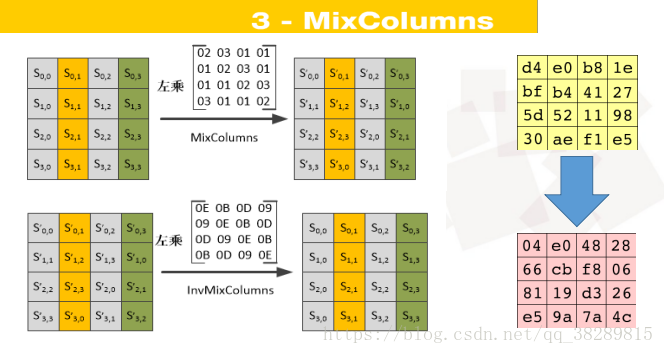
mix_column_matrix = [0x2, 0x3, 0x1, 0x1, 0x1, 0x2, 0x3, 0x1, 0x1, 0x1, 0x2, 0x3, 0x3, 0x1, 0x1, 0x2] # 列混合乘的矩阵
i_mix_column_matrix = [0xe, 0xb, 0xd, 0x9, 0x9, 0xe, 0xb, 0xd, 0xd, 0x9, 0xe, 0xb, 0xb, 0xd, 0x9, 0xe] # 列混合乘的逆矩阵
def gen_key(key):
key_hex = get_hex(key)
key_rotate = []
w = [[] for i in range(0, 44)]
for i in range(0, 16):
w[i // 4].append(key_hex[i])
for i in range(4, 44):
gw = copy.deepcopy(w[i - 1])
if i % 4 == 0:
gw[0], gw[1], gw[2], gw[3] = gw[1], gw[2], gw[3], gw[0]
gw = substitute(gw) #g(w(i-1))
gw[0] = hex(int(gw[0], 16) ^ rcon[i // 4 - 1]) #ppt上说的2^(i-4)/4有误,看书p84
for j in range(0, 4):
w[i].append(hex(int(gw[j], 16) ^ int(w[i-4][j], 16)))
key_rotate = [w[i * 4] + w[i * 4 + 1] + w[i * 4 + 2] + w[ i* 4 + 3] for i in range(0, 11)] # 轮密钥列表,每个元素都是有16个字节的列表
return key_rotate
def xor(a, key): #a和key都是列表,都存了16字节
return [hex(int(a[i], 16) ^ int(key[i], 16)) for i in range(0, 16)]
def get_hex(s): #得到一个字符串的十六进制值,以列表形式返回
return [hex(ord(i)) for i in s]
def shiftrows(a, inverse=False): #inverse为True时表示为逆操作,默认为False
return [ a[0], a[5], a[10], a[15], a[4], a[9], a[14], a[3], a[8], a[13], a[2], a[7], a[12], a[1], a[6], a[11] ] if not inverse else [ a[0], a[13], a[10], a[7], a[4], a[1], a[14], a[11], a[8], a[5], a[2], a[15], a[12], a[9], a[6], a[3] ]
def mixcolumn(m_row, inverse=False):
matrix = mix_column_matrix if not inverse else i_mix_column_matrix
m_col = []
for i in range(0, 16):
x, y = i % 4, i // 4
result = 0
for j in range(0, 4):
result ^= (mul(matrix[x * 4 + j], int(m_row[y * 4 + j], 16)))
result = mod(result)
m_col.append(hex(result))
return m_col
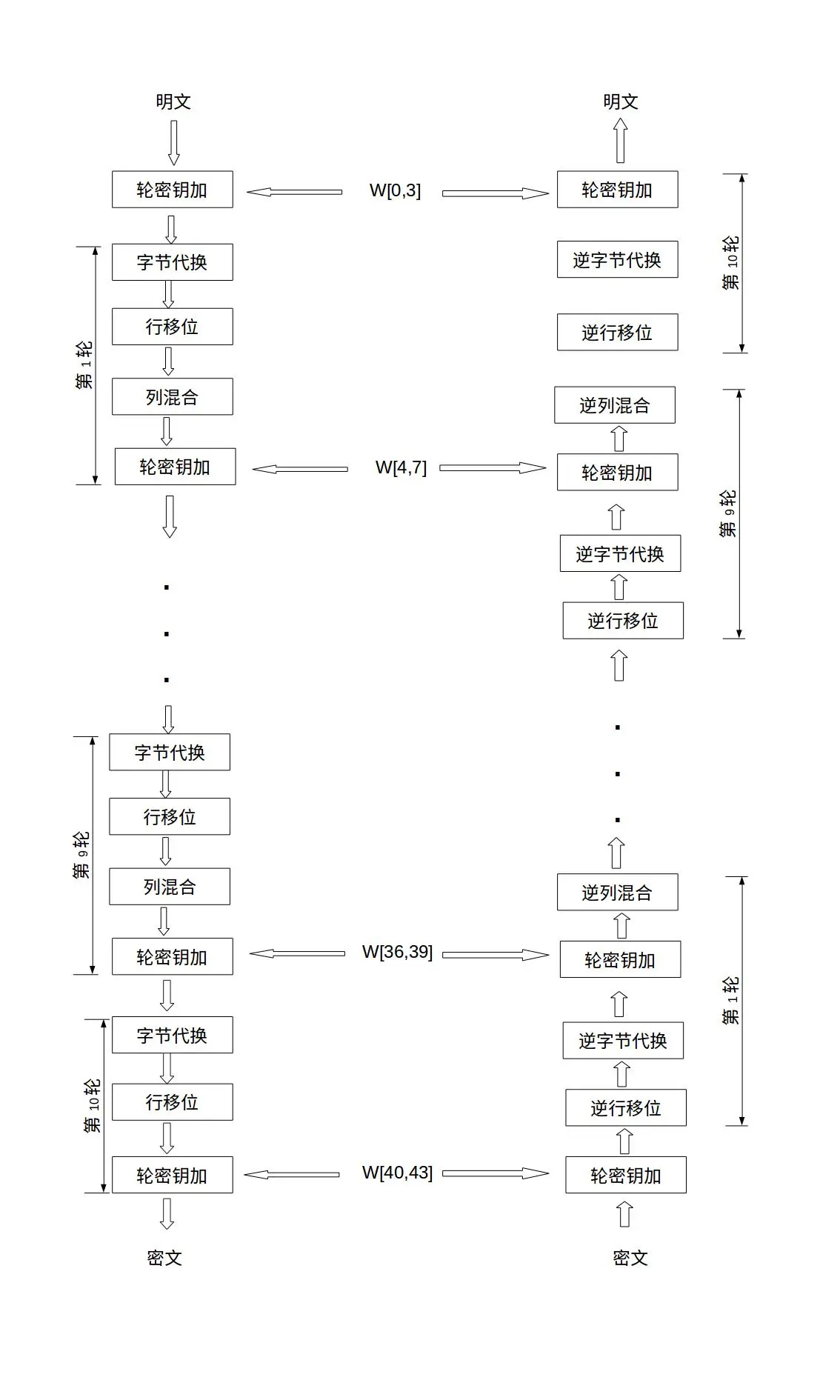
def aes_encrypt(m, key_rotate):
m_hex = get_hex(m) #得到明文的hex列表
m_xor = xor(m_hex, key_rotate[0]) #将明文初始xor密钥 w0 w1 w2 w3
for rotate in range(1, 11): #十轮
m_s = substitute(m_xor) # 字节代替
m_row = shiftrows(m_s)
m_col = m_row #列混合
if rotate != 10: #最后一轮不用列混合
m_col = mixcolumn(m_row)
m_xor = xor(m_col, key_rotate[rotate])
ciphertext = "" #输出的密文为每个十六进制字符的联结,类似e365e09962d634a8fbfe8359c57b22c5。一共32个,每两个字母对应了一个字节的十六进制。16个进制,128位。
for i in m_xor:
ciphertext += (i[2:] if len(i[2:]) == 2 else "0" + i[2:]) #对类似0xf的十六进制格式化为0x0f
return ciphertext
def aes_decrypt(c, key_rotate):
c_hex = ['0x' + c[i * 2] + c[i * 2 + 1] for i in range(0, 16)] #将密文恢复为列表
c_xor = xor(c_hex, key_rotate[10])
c_row = shiftrows(c_xor, inverse=True)
c_s = substitute(c_row, inverse=True)
for rotate in range(9, 0, -1): #循环9次
c_xor = xor(c_s, key_rotate[rotate])
c_col = mixcolumn(c_xor, inverse=True)
c_row = shiftrows(c_col, inverse=True)
c_s = substitute(c_row, inverse=True)
plaintext = ""
for i in xor(c_s, key_rotate[0]): #将明文的hex列表转化为字母
plaintext += chr(int(i, 16))
return plaintext
# 原始明文和密钥
m = "1234567890abcdef"
key = "1234567890abcdef"
# 生成轮密钥
key_rotate = gen_key(key)
# 加密
ciphertext = aes_encrypt(m, key_rotate)
print("Ciphertext:", ciphertext)
# 解密
plaintext = aes_decrypt(ciphertext, key_rotate)
print("Decrypted text:", plaintext)
|