DSA签名算法
DSA签名算法
DSA算法简介
DSA(Digital Signature Algorithm)是Schnorr和ElGamal签名算法的变种,被美国NIST作为DSS(DigitalSignature Standard) 数字签名的标准。
DSA是一种更高级的验证方式,它是一种公开密钥算法,不能用来加密数据,一般用于数字签名和认证。DSA 不单单只有公钥、私钥,还有数字签名。私钥加密生成数字签名,公钥验证数据及签名。在DSA数字签名和认证中,发送者使用自己的私钥对文件或消息进行签名,接受者收到消息后使用发送者的公钥来验证签名的真实性,包括数据的完整性以及数据发送者的身份。如果数据和签名不匹配则认为验证失败!数字签名的作用就是校验数据在传输过程中不被修改。
DSA数字签名可以理解为是单向加密的升级,不仅校验数据完整性,还校验发送者身份,同时还由于使用了非对称的密钥来保证密钥的安全,所以相比消息摘要算法更安全。
DSA只是一种算法,和RSA不同之处在于它不能用作加密和解密,也不能进行密钥交换,只用于签名,它比RSA要快很多。
DSA算法签名的过程
- 使用消息摘要算法(例如sha-256/md5)将要发送数据加密生成信息摘要。
- 发送方用自己的DSA私钥对信息摘要再加密,形成数字签名。
- 将原报文和加密后的数字签名一并通过互联网传给接收方。
- 接收方用发送方的公钥对数字签名进行解密,同时对收到的数据用消息摘要算法产生同一信息摘要。
- 将解密后的信息摘要和收到的数据在接收方重新加密产生的摘要进行比对校验,如果两者一致,则说明在传送过程中信息没有破坏和篡改;否则,则说明信息已经失去安全性和保密性。
算法原理
DSA是证书基于有限域离散对数的难题。
- 相关参数
p:一个素模数,其值满足:$2^ {L-1}<p<2^L,$ L是64的倍数满足512<=L<=1024
q:(p-1)的素数因子,其值满足2^159^<p<2^160^ 即q长度为160.
g:g=pow(h,(p-1)/q,p).h满足1<h<p-1 的任意整数,从而有pow(h,(p-1)/q,p)>1
x:私钥。x为一个伪随机或随机生成的整数,其值满足0<x<q
y:公钥。y=pow(g,x,p)
- DSA签名过程:
- 产生一个随机数k,其值大小满足0<k<q。
- 计算r=pow(g,k,p) mod p,其值满足r>0
- 计算$S=(K^{-1}(SHA(M)+x*r))mod q$,其值满足s>0
$k^{-1}$表示整数k关于某个模的逆元。k在每次签名都重新生成
sha(M):M的hash值,M为待签名的明文,sha是一个单向散列函数。SHA(M)是一个长为160bites的字符串。
4。 最终签名是证书对(r,s),它们和M一起发送到验证方
- 尽管 r 和 s 为 0 的概率相当小,但只要有任何一个为 0 ,必须重新生成 k,并重新计算 r 和 s
- DSA验证签名过程
w=s^-1^(mod p);计算u1=SHA(M)*w(mod p)
u2=r*w(mod q)
v=(g^u1^y^u2^(mod p))(mod q)
验证v=r
r=pow(g,k,p)(mod q)
我们要证v=r, 只需证明$g^{u1}⋅y^{u2}≡g^k(modp)mod q$
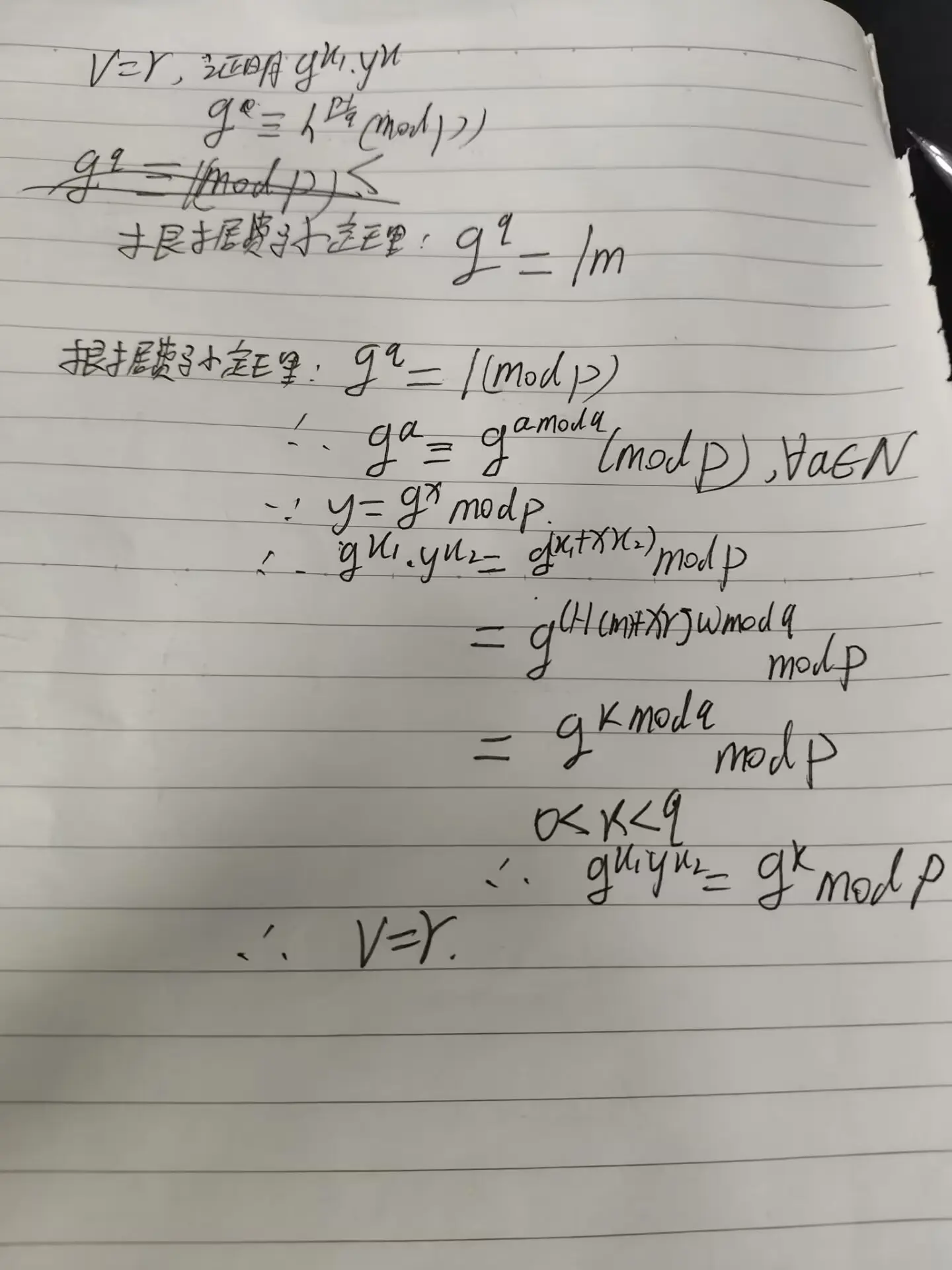
一道关于签名的题
1 | |
欧拉定理的应用。
如果a=b mod(ϕ(n))
那么r^a=r^b(mod n)
关于r,因为r>1。r^t+1为素数
当t=1时,r=一个素数-1有无数中情况
当t!=1,r^t^+1=(r-1)(r^t-1^+r^t-2^+…+r-1)。r>1,仅当r=2时r-1=1,才可能出现r^t^+1为质数。
sign=flag^d2^*pow(r,e^3^+d^6^,n)(mod n)
利用欧拉定理化简,ed=1mod(ϕ(n))
sign=flag^d2^*pow(r,e+Gensin_imapct-7,n)mod(n)
解题代码
2
3
4
5
6
7
8
9
10
11
12
13>from Crypto.Util.number import long_to_bytes, inverse
>n = 19639600328223844671704489123546988501903291473349872361018733749009923532016394909567762757637482279817331983071860682071520655098361565285241715414618380704335591153776055798928550295962562555560982153165980397579235902710145810308858838361625306321488259768221057352332575949434950772126970211685369981876613470725028558324654396470304051821380286349980490471220545022189063994727777531050923387558677338680506629547393515821317364707844365033855139133865759355286813851518294897143238579929549731310223985355362071605128276336758148702451325980353936486982957612319356732811212155843888427077650287475747285951601
>Gensin_imapct= 18615555428360737203858483119761379803106644123408751679939358715271019322622307162405939351971133494343617187336142906474728142088496643169394250609891618465867143428166101133715080086728905605225823417826656587225513551367394290013533665519042222764801563252344045263175116633786657350554126906044647802447911150169379968579328635616455291791600544040115862318977749381935402023854289083858694560732129788448185879164909390679473356534896789097443806715065702402663094294822600231699016344340995159197584811683173565575413157051411913858323747295630124277461052366727340740896932709939898865571387315262920418086796
>r=2
>e=65537
>sign = 18261288204538981181572030482759798426584790136542118628596729895932121795847442916705403582815245847900360562985283644900159284591973184497644109333171698289712411404441725787627481262217515952804383265861395076527124697355904244489084976865989880843929716655444342667450793474028911238581561497418112019001371342787536639006129163007454921434977528441447969586481438173863864729524626228931577767719945486242388940962427531910977068386343876595966004145276572320724583981474334914270335016486389617018440139421924715459467601533349012045847315524603087767378612501984188376727698068090618376138788002607182927230811
>flagd2=sign*inverse(pow(r,e+Gensin_imapct-7,n),n)
>flag=pow(flagd2,e**2,n)
>print(long_to_bytes(flag))
>'''
>b'SYC{G0od_Math_h3lps_S1gnature_in_RSA}'
>'''