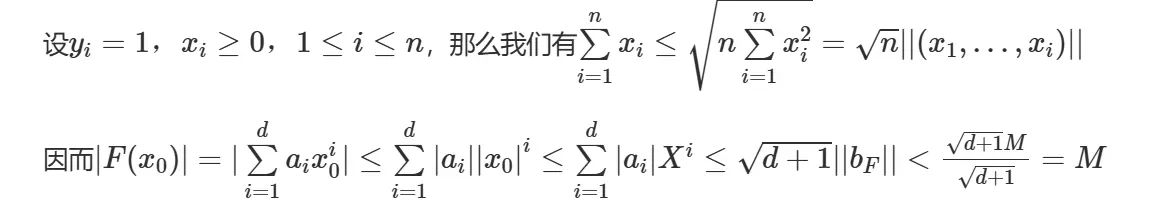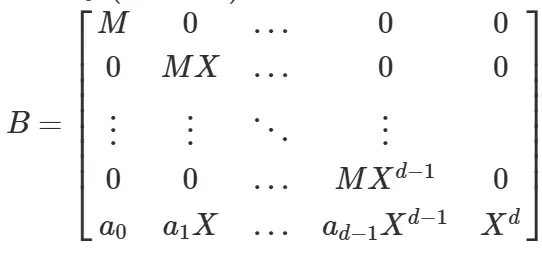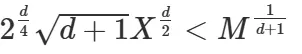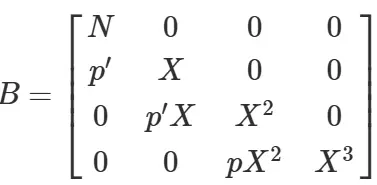coppersmith方法相关

coppersmith

原论文ch19.pdf

借鉴博客：https://jayxv.github.io/2020/08/13/%E5%AF%86%E7%A0%81%E5%AD%A6%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0%E4%B9%8Bcoppersmith/

  • 前言

最近经常遇到coppersmith攻击，所以决定还是有必要深入学习一下

coppersmith’Method

介绍：coppersmith方法基于格约简和LLL算法来找到一定模数下多项式的小根。其核心思想是将求解模多项式方程的问题转化为一个格中的短向量问题

例如F$F(x)=x^3+x+123(mod M)$,M=77,假设存在x0使得$F(x_0)=0$

并且这个x0小于某个特定值，就可以使用coppersmith算法

给定模M的多项式$F(x)=x^d+a^{d−1}x_{d−1}+⋯+a^1x+a^0$,[必须让$x^d$满足系数为1，可以乘$a_d^{-1}$来配凑。如果ad没有模M逆元，可以拆分为多组。

假设我们知道$F(x_0)=0(mod M)$ ,并且|$x_0$<$M^{1/d}$

假设我们现在能找到G($x_0$)=0,不需要取模，我们可以用coppersmith方法把这个F(x)变为G(x)

例如$M=17*19=323$,$F(x)=x^2+33x+215,$,假设一个小根$x_0=3$但是在整数

域下F(3)!=0,所以我们要找到G(3)=0,

$G(x)=9⋅F(x)−M⋅(x+6)=9x^2−26x−3$，满足G(3)=0,

这是一元coppersmith的核心思路。

  • 为什么造格能得到较小的G(X)

设F(x)构造系数矩阵为A,x=(x,x,x)

G(x)系数矩阵,L=UA。$A*x=(ax+bx+cx)=(0)mod(m)$

$Lx=U(AX)=U(0)=0mod(m)$

依然满足f(x0)=0,G(x0)=0,mod(m)

  • 我们现在主要要找x0的界，设X是|x0|的上界

F(x)可以表示为一个行向量$B_F=(a_0,a_1X,a_2X^2,…,a_dX^d)$

首先我们有F(X),M,B_F,X—-$F(x_0)=0(mod M)$

那么当$|B_F|<M/(d+1)^{0.5}$,则有F(x0)=0接下来证明它

  • 引入柯西不等式–1式子

$(∑^n_{i=1}x_iy_i)^2≤(∑^n_{i=1}x^2_i)(∑^n_{i=1}y^2i)$

所以$-M<F(x_0)<M$ 且F(x0)=0 mod M 所以F(X0)=0

  • 确定边界值X

X为x0取值上界，这!个矩阵$det(L)=M^dX^{d(d+1)/2}$

我们可以利用格基规约找到最小的第一行b’,格的部分不多叙述可以参考写的LLL的速通blog

之后我们可以得到在满足1式子的条件下

可以得到X的大致范围

示例M=10001,多项式$F(x)=x^3+10x^2+5000x−222$

确定$x_0<M^{1/6}$,这里省略了相差无几的系数。确定上界为5左右

我们这是可以构造矩阵然后格基规约。

第一行便是所需求满足要求的最小$G(x)=444+x−20x^2−2x^3$

接的x0=4

  • The Full Coppersimth Method

一个关于提高X大小的方法，有两个方法我们称这种往格里插入的，增加了格的维度而不增加M的多项式为：“x-shift” polynomial，它们是$xF(x),x^2F(x),…,x^kF(x)xF(x)$，显然这些多项式在M下的解也为x0

针对第二种方案，我们可以利用F(x)F(x)的幂来增加M，因为F(x0)≡0(modM)F，则有$F(x0)^k≡0(modM^ k)$

  • 另一个定理

设$0<ϵ<min0.18,1/d,F(x)$度为d的首一多项式如果在域下有一个或多个跟x0满足$|x0|<M^{1/d-ϵ}$ .那么我们就可以在与d,1/ϵ,log(M)相关的多项式时间内找到x0.

证明有点抽象了论文放这里有空再瞅瞅吧，我直接写下几个脚本用得到的关系式子

h≈$1\over {dϵ}$ ，dh=n表示格的维度。

  • 关于已知p部分信息分解n

设$N=p∗q$并且有$p<q<2p$，设$0<ϵ<14$4，如果满足关系：$|p−p′|≤$$$1\over{2\sqrt{2}} $$$$N^{1/4−ϵ}$$，那么给定N和p’,我们就可以在与log(N)和1/ϵ相关的时间复杂度内分解N。原理证明有点奥了

举例:N=16803551，p′=2830，X=10.

设F(x)=(x+p’),N,F(x)，xF(x)=(x2+p′x)，x2F(x)

考虑多项式：N,F(X),xF(x),$x^2F(X)$,然后构造格

LLL规约后得到第一行的SVP为（105，-1200，800，1000），去除X=10可以得到G(x)=x3+8x2−120x+105；解的x=7，

这里的N可以看作kp，把它看作是k∗p也许会好理解些：所选取的多项式带入正解x时均在模p下与0同余

一些题目(单元coppersmith)

已知P高位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from Crypto.Util.number import getPrime, bytes_to_long, inverse

flag=b'fox{fox want to eat what}'
p=getPrime(512)
p_high=(p>>200)<<200
print(p_high)
q=getPrime(512)
e=0b10001
n=p*q
print("p=",p)
print("q=",q)
print("n=",n)
m=bytes_to_long(flag)
c=pow(m,e,n)
print("c=",c)

解密代码，这里引用的beta表示N与p的指数关系在(0.4,0.5）而且一般已知p的信息的比特位数要为p本身比特位数的一般以上调整beta可以增加上限X但是会导致时间复杂度增大，,另外其实还要一个ϵ(epsilon)用来约束多项式的根，一般设置在0.01到0.05的样子，也可以在这个现成的函数中设置，越小约束越严格但是也会影响运算时间

可以在这个脚本实现源码看看，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
N=133710312641113123859964440077377533712342702504367787255182846824724010714496099762855320340674761905445770124260476807002239449704342315985473499561372208925050652507764912706096791716888012136098375017749241890296762979638092647971448134034808167719762321413756060356748672986521523183243757912647146630053
e=0b10001
c= 65557915039839389047479107840683903322175662706377407690136936904175441214121027091201698676495252709350177099515464449769710120030105578393734170368995189857074788448412022342701700787139604106626472335713315769690072453661188617266051033715771747892127805257411819414888757977975890254221744212355033949446

p1=10588155095945660931536816256842811488117167553129301589697663144204701166787360146714639470812049936139282091010528731135222839016760257988792628488962048
ZmodN = Zmod(N)
P.<x>=PolynomialRing(ZmodN)
f=p1+x
x0=f.small_roots(X=2^200,beta=0.4)
p=p1+x0[0]
p=int(p)
q=N//p
h=(p-1)*(q-1)
d = inverse_mod(e,h)
m=int(pow(c,d,N))
print(long_to_bytes(m))
  • 补充，如果是求低位可以,``设f=p+x*2^kbits,然后f = f.monic()化系数为1

已知d低位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import getPrime, bytes_to_long, inverse

flag=b'fox{fox want to sleep}'
p=getPrime(512)
q=getPrime(512)
e=49
n=p*q
print("p=",p)
print("q=",q)
print("n=",n)
m=bytes_to_long(flag)
d=inverse(e,(p-1)*(q-1))
d0=d&((1<<512)-1)
print("d0=",d0)
c=pow(m,e,n)

print("c=",c)

已知d的低512位，需要先推导求出p低位然后再利用p低位求法求出p

k必然是小于e的所以()如果e比较小可以用爆破，而且得到的p0不一定就是低位所以需要和n求公约数计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import *
def re(p0,n):
    P.<x> = PolynomialRing(Zmod(n))
    pb=p0.nbits()
    nb=n.nbits()
    f = p0 + x*2^pb
    f = f.monic()
    r = f.small_roots(X=2^(nb//2-pb),beta=0.4)
    if r:#不一定是p0所以需要爆破一下
        x0 = r[0]
        p = gcd(x0*2^pb + p0, n)
        return ZZ(p)
def re_p0(d0,e,n):
    X=var('X')
    for k in range(1,e+1):
        res=solve_mod([e*d0*X == k*n*X + k*X + X-k*X**2 - k*n],2^d0.nbits())
        for x in res:
            p0=ZZ(x[0])
            p=re(p0,n)
            if p and p!=1:
                return p
e=49
n= 109414997218017430689750411358870671148755060537823638639312822690278731526747343386131161374178565377568510541067027291819153801268584631898655552531100229691697272740485676268557392576883083322538380985686287633325507643109809662875001865516112341416350089749503409352233344213405771505339817806009334467873
d0= 6589907493136215112152812078061957297077302140846480772722502061060417041525745970773308362109848374417314681016788951311262599036142398830169352909596817
c= 52618099026096173424982985915057984673936322178451784029192431909399153643977616885476290932528093004726036699015260255387007582939696987106414732619027888230272826489001101650428442052309028725473145170506018789419664921530741182296203037987680548988272155176048872109505915948350201120031522636544622010733
p=re_p0(d0,e,n)
q=n//p
d=inverse_mod(e,(p-1)*(q-1))
m=pow(c,d,n)
print(long_to_bytes(m))

’‘’
一般来说e是素数但是我当时应该是写错了题目脚本但是仍然能跑
‘’‘

已知d高位

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
from secret import m1
def task1():
    e = 149
    p = getPrime(512)
    q = getPrime(512)
    n = p * q
    d = inverse(e,(p-1)*(q-1))
    return (pow(m1, e, n), d >> 222 << 222, n)
    
c1, leak1, n1 = task1()
print(c1, leak1, n1)
# (89623543982221289730635223555830551523170205418976759060541832483843039074358160566735322009158596405712449020903311144480669706226166537602750967447480664875090686428406188847601970724994074417752345460791736191511081890913041143570455636020205647345764692062144226011846336769477026234106683791286490222089, 138474880017294332349992670187778287774153347391371789199005713563195654993662610111557185709277805165708109047494971468100563949333712521647405765501704478862377527360106399421209690341743821320754482338590671565510629203215009008479290995785318405211007685664887994061938667418220613430135743123498167435264, 146331610798417415036517077006943013321623040860385791423062775325646472298267580898028515394910588437521335092742913111680737790430660749825981979147191282007208147041227246620008377726207734522466015971515317594545750944838673018946440525615131606652748549901880641896940968837669894325535750125282351577689)

这里l e a k d = d > > 222 < < 222

和上面计算低位方法类似但是这里得到到p不一定是p高位，这里的省略之类的不算很明白

有点抽象了，不太理解这里高位的误差。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import *
def full_p(p_high, n,d_high,bits):
    PR.<x> = PolynomialRing(Zmod(n))    
    f = x + p_high
    f = f.monic()
    roots = f.small_roots(X=2^(bits + 4), beta=0.4)  
    if roots:
        x0 = roots[0]
        p = gcd(x0 + p_high, n)
        return ZZ(p)


def p_high(d_high, e, n,bits):
    PR.<X> = PolynomialRing(RealField(1000))
    for k in tqdm(range(1, e+1)):
        f=e * d_high * X - (k*n*X + k*X + X-k*X**2 - k*n)
        results = f.roots()
        if results:
            for x in results:
                p_high = int(x[0])
                p = full_p(p_high, n,d_high,bits)
                if p and p != 1:
                    return p


c1 = 89623543982221289730635223555830551523170205418976759060541832483843039074358160566735322009158596405712449020903311144480669706226166537602750967447480664875090686428406188847601970724994074417752345460791736191511081890913041143570455636020205647345764692062144226011846336769477026234106683791286490222089
leak1 = 138474880017294332349992670187778287774153347391371789199005713563195654993662610111557185709277805165708109047494971468100563949333712521647405765501704478862377527360106399421209690341743821320754482338590671565510629203215009008479290995785318405211007685664887994061938667418220613430135743123498167435264
n1 = 146331610798417415036517077006943013321623040860385791423062775325646472298267580898028515394910588437521335092742913111680737790430660749825981979147191282007208147041227246620008377726207734522466015971515317594545750944838673018946440525615131606652748549901880641896940968837669894325535750125282351577689
e1 = 149
p1 = p_high(leak1, e1, n1,222)
q1 = n1 // p1
d1 = inverse(e1,(p1 - 1) * (p1 - 1))
m1 = pow(c1,int(d1),n1)
print(m1)

SU_rsa

应该算是比较容易分析的简单rsa

由于给的是d的高位，直接可以用得到k(这算是一种整除，当时确实没想到这种方法，因为n和p,q,k差值过大所以k可以利用整除求出来)
$$
k=(ed_m-1)//n + 1
$$
由标准关系得到
$$
k(n-p-q+1)+1==e*d\
(p+q) =(n+1+k^{-1})\mod e
$$
相当于给出了p%e或者q%e的值，e为256bits，显然small_roots求解一下就行。

值得注意的是，这里由于取的低位比较小，已知信息比较少，需要爆破

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from Crypto.Util.number import *

d_m =  54846367460362174332079522877510670032871200032162046677317492493462931044216323394426650814743565762481796045534803612751698364585822047676578654787832771646295054609274740117061370718708622855577527177104905114099420613343527343145928755498638387667064228376160623881856439218281811203793522182599504560128
n =  102371500687797342407596664857291734254917985018214775746292433509077140372871717687125679767929573899320192533126974567980143105445007878861163511159294802350697707435107548927953839625147773016776671583898492755338444338394630801056367836711191009369960379855825277626760709076218114602209903833128735441623
e =  112238903025225752449505695131644979150784442753977451850362059850426421356123
k = (e*d_m-1)//n + 1
s = (n+1+inverse_mod(k, e))%e
PR.<x> = PolynomialRing(Zmod(e))
f = x^2-s*x+n
p0 = int(f.roots()[0][0])
print(p0)
import multiprocessing
import tqdm
from hashlib import sha256
def copper_attack(i):
    PR.<x> = PolynomialRing(Zmod(n))
    f = e*(2^12*x + i) + p0
    f = f.monic()
    res = f.small_roots(X=2^244, beta=0.499, epsilon=0.02)
    if(res != []):
        t = int(res[0])
        p = e*(2^12*t + i) + p0
        q = n // p
        assert p * q == n and isPrime(p) and isPrime(q)
        print(b'SUCTF{',sha256(str(p).encode()).hexdigest()[:32],b'}')
        print(b'SUCTF{',sha256(str(q).encode()).hexdigest()[:32],b'}')
        return True

with multiprocessing.Pool(processes=16) as pool:
    for _ in tqdm.tqdm(pool.imap(copper_attack, range(2^12)), total=int(2^12)):
        if(_):
            break#多线程
python > crypto
#crypto #python
coppersmith方法相关
http://example.com/2025/01/23/copper/
Beitragsautor
fox
Veröffentlicht am
January 23, 2025
Urheberrechtshinweis