一篇文章速通群论

群论

群基础

群的基本定义

代数系: 设S表示一个非空集合，那么$S * S->S$ 的映射叫做S的结合法或运算$SS->S$, $(a,b)->ab$ 其中a,b∈S集合(这里的号不是乘法，只是一种计算方式)如果这个S满足封闭性(任意上述a*b∈S)。

这样的S叫做一个代数系，当然这只是为了方便我们理解群的性质

半群:如果这个S满足结合律。

结合律: (ab)c=a(bc)

这个S就称为半群
含幺半群:

这里我们需要理解一个很重要的概念，幺元。

设非空集合S，存在S上的一个二元运算”.” ，对于元素$e∈S$，若对于∀a∈S，都有$ea=a$ ，则称e为S的左幺元，同理∀a∈S，都有ae=a，则称为S的右幺元，若e既是左幺元又是右幺元$(ea=ae=a)$，则称e为S的幺元(单位元)。

幺元(单位元):通常记为e，设a∈S，$ae=ea=a$, 有幺元的半群叫做含幺半群

群:

群就是含有逆元的含幺半群，

逆元:任意a,b∈S,存在 a和b的逆元分别记作,a^-1^,b^-1^ 。

并且$a*a^{-1}=e$

总结下来，群的定义如下

一个集合 GG 和一个二元运算 :$G×G→G→G$，构成一个群 (G,∗)，当且仅当满足：

封闭性。对于任意 g,h∈G，g∗h∈G。这其实是代数系统的要求。
结合律: $(a∗b)∗c=a∗(b∗c)$。
存在单位元 e∈G，使得群中任意元素 g∈G 都满足 $e∗g=g$。
逆元:对于群中任意元素 g∈G，都存在逆元 g^−1^∈G 满足 g^−1^∗g=e

阿贝尔群:满足交换律的群
有限群与无限群:根据群中元素的个数来判断

满足交换律的群:任意a,b∈G,都存在ab=ba

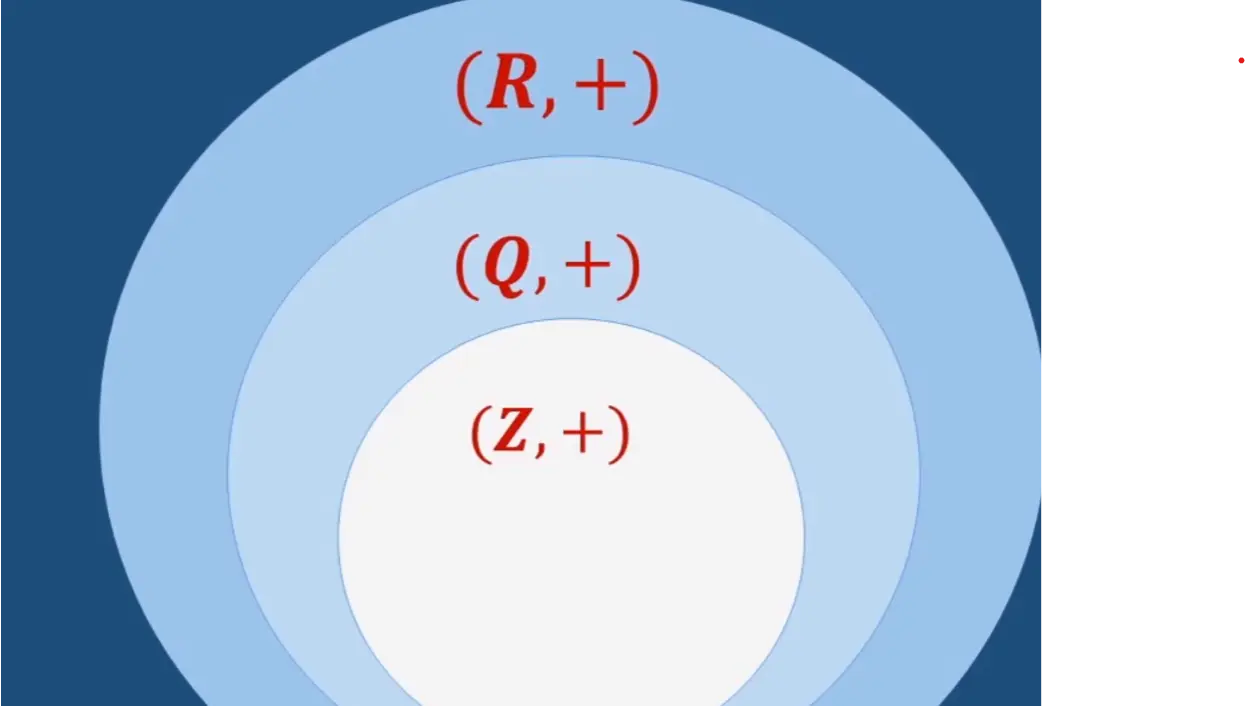
举个群的例子:

整数加法群(Z,+)

任意两个整数相加，结构都是唯一的整数。(满足封闭性)

整数加法满足结合律(满足结合律)

整数的单位元是0，任何整数加0都是0(有幺元)

整数加法中一个数的相反数是他的逆元，他们相加便是单位元0(有逆元)

并且整数群还满足交换律。所以它是个阿贝尔群

乘法群

如果是一个整数乘法，1就是单位元，但是不是所有数都有逆元，比如4的逆元1/4就不属于整数群。

但是有理数乘法群G(Q,*)是存在的。

群的性质

一些性质

单位元唯一

证明: 设e1,e2是群G的唯一单位元，则,e1=e1*e2=e2

逆元唯一

证明：对于群G中的元素g∈G,如果h1,h2是g的逆元。则$h_1=h_1e=h_1gh_2=eh_2=h_2$

对于a,b∈G，有且只有一个c∈G满足ac=b。

证明: 取c=a^-1^ b。

唯一：如果ac=b,则c=ec=a^-1^ ac=a^-1^b .

(a*b)^-1^=b^-1^ a^-1^

证明: $b^{-1}a^{-1}ab=b^{-1}b=e=a^{-1}a=abb^{-1}a^{-1}$

计算性质

(1)$a^n a^m=a^{m+n}$

(2)$(a^{n})^m=a^{mn}$

(3)$(a^{-n})^m=a^{-mn}$

(4)$(a^n)^{-m}=a^{-mn},(a^{-n})^{-m}=a^{mn}$

群和元素的阶

一个群如果含有有限个元素，则称为有限群，否则称为无限群，通常用|G|来表示群G的元素个数，也称为群的阶。

元素的阶: 设$G$是群，$a∈G$，如果n是满足$a^n=e$的最小的正整数，则称n是元素a的阶。

子群

子群定义

设(G,*)是群，H是G的非空子集，如果(H,*)构成一个群，那么称(H,*)是一个群，则称(H,*)是(G,*)的子群。

平凡子群:({e},*)(只有单位元)，(G,*)(G本身)

其他,非平凡群

示例

加法实数群(R,+)，那么加法有理数群(Q,+)是它的子群，加法整数群(Z,+)也是它们的子群

子群的单位元

定理:H是群G的子群，e∈G是单位元，则e也是子群H的子群

证明: 假设H的单位元是e^’^，同时e≠e^’^。对于a∈H,e^’^a=a=ea。所有e^’^=e

子群的逆元

定理: H是群G的子群，a∈H，则a^-1^∈H。

证明:

假设b∈H,a∈H,b≠a。a*b=e

同时a*a^-1^=e=a*b 所有a^-1^=b

判断子群

H是群G的非空子集，对于任意a,b∈H,都有a*b^-1^∈H，则H是G的子群
根据定义:设(G,*)是群，H是G的非空子集，如果(H,*)构成一个群，那么称(H,*)是一个群，则称(H,*)是(G,*)的子群。
H是群G的非空子集，如果H是有限集，而且群G的运算*在H上满足封闭性，则H是G的子群。

子群的构造

阿贝尔群的子群构造

定理:G是阿贝尔群，m∈Z,则$G^m=[a^m|a∈G ]$是G的子群

证明: a,b∈G,则a^m^，b^m^ ∈G。

a^m^*(b^m^)^-1^ =(a*b^-1^)^m^

示例:加法整数群(Z,+)

3Z可以表示它的子群(3Z,+)={0,±3,±6,..,±3n}

定理G是阿贝尔群，m∈Z，则G{m}={a∈G|a^m^=e}是子群

证明:

a,b∈G，a^m^=b^m^=e,则a,b∈G{m}

因为$(ab^{-1})^m=a^m(b^{-1})^m=e*e=e$∈G{m}

即证

整数的子群
1. H是$Z_n$(模n的加法)的子群，则存在唯一非负整数m，使得H=mz。

$\mathbb{Z}_n是有限循环群，由 1 生成，即 \mathbb{Z}_n = <1>$。

有限循环群的每个子群也是循环群，对应于 ( n ) 的因子。

所以 ( H ) 一定是某个 ( m ) 的倍数集合：
[
$H = \langle m \rangle = m\mathbb{Z}_n = { mx \bmod n \mid x \in \mathbb{Z} }$
]

唯一性来自最小正生成元的唯一性。

m1和m2是非负整数，当且仅当$m_1Z_n⊆m_2Z_n$，有m2|m1

$m_2Z_n$ 可以看作加法群(G,+)，根据上面阿贝尔群子群的构造中的定理有

任意k⊆Z,使得$kG=m1/m_2G=m_1Z_n⊆G$

，则有m2|m1。反之，设 $m_1=m_2q$，

则有$m_1Z_n=m_2qZ_n={m_2qx|x∈Z_n}⊆m_2Z_n$

所以$m2∣m1⟺m1Zn⊆m2Zn$

举例,9Z={0,±9,±18..,±9n]是3Z={0,±3,±6,±9,…±3n}的子群。

子群构造子群

定理1**:H₁和H₂ 是阿贝尔群G的子群，则$H=H_1H_2$ 也是G的子群**
$$
H=H_1H_2={a_1a_2|a_1∈H_1,a_2∈H_2}
$$

证明

H非空，因为H₁ H₂ 都是非空的。

对于任意a,b∈H,那么有$a=a_1a_2,b=b_1b_2且a_1,b_1∈H_1,a_2,b_2∈H_2$

$ab^{-1}=(a_1a_2)b_2^{-1}b_1^{-1}=(a_1b_1^{-1})(a_2*b_2^{-1})∈H$ –>因为满足交换律

通常，H1*H1≠2H1

例:(Z,+) ，Z+Z构成的子群还是是(Z,+)，而（2Z,+)是{0,±2,..,±2n)。

扩展: H₁，H₂…H_n 是阿贝尔群G的子群，则$H=H_1H_2..H_n$ 也是G的子群

定理2: H1和H2是G的子群，则H=H1∩H2也是G的子群

$H=H_1∩H_2={a|a∈H_1,a∈H_2}$

证明:H非空(因为e∈H1，H2)

那么定义a∈H1，H2;b∈H1，H2。

a*b^-1^∈H1，a*b^-1^∈H2。那么a*b^-1^∈H。

扩展:存在H1，H2…,Hn是G的子群 $H_1∩H_2∩…∩H_n=H$ 也是G的子群

定理3:H1和H2是群G的非平凡子群，那么

$G≠H_1∪H_2$

证明:

假设G＝H1∩H2。

因为H1是非平凡子群，所以∃a∈G但事实a∉H1。和b∈G但是b∉H2.

因为G=H1∪H2，所以，a,b∈H1∪H2

那么有a∈H2，b∈H1。

考虑a*b=c∈G,那么a*b必定属于H1或H2

假设c∈H1，

因为b∈H1，c∈H1，且根据子群的定义和性质

则有c*b^-1^=a∈H1，显然矛盾

同理假设c∈H2

因为a∈H2，c∈H1，且根据子群的定义和性质

则有c*a^-1^=b∈H2，显然矛盾

正规子群和商群

陪集(coset)

陪集的定义

( [这里的a*b表示进行的群内的’*‘运算，不是乘法，也不是像之前整数加法子群里面的让Z群内的元素进行a次运算])定义:

H是群G的子群，a∈G，

则有 $aH={a*h|h∈H}$,称为H关于a在G中的左陪集。

$Ha={h*a|h∈H}$，称为H关于a在G中的右陪集。

如果Ha=aH，称为H关于a在G中的陪集

a称为代表元

陪集:[a]_H ，左陪集:aH ，右陪集: Ha。

为了方便，后面统一称呼配给-[a]_H

示例：3Z={0,±3,…,±3n}.是加法群(z,+)的子群

陪集:

[0]_3Z={0,0±3,…,0±3n}

[1]_3Z={1,1±3,…,1±3n}

[2]_3Z={2,2±3n,…,2±3n}

[3]_3Z={0,0±3n,…,±3n}

……

可以看到每个整数只会出现在唯一的陪集中(除了相同的陪集[0]_3Z和[3]₃这种完全相等的陪集外，其他任何陪集之间交集都为空)。陪集就是对群进行的划分。

解释:陪集通过群的子群对群进行划分。可以看做是一种距离,这个子群3Z作为对群(Z,+)的一种划分标注能和依据。

[0]_3Z到3Z的元素的距离是0表示3Z本身，[1]_3Z到3Z中元素的距离是1，[2]_3Z到3Z中元素的距离是2

这三个集合取并集:[0]_3Z∪[1]_3Z∪[2]_3Z=(Z,+)。并且之间两两交集为0

陪集的性质

性质1:**a∈[a]H(每个元素必然会进入子集构造的陪集里)**。

H={e,….},那么[a]_H={a*e,…}={a,…}

性质2:[e]_H=H(用单位元构造的陪集等于子群本身–平凡陪集)。

[e]_H={…,e*h,…}={…,h,…}

性质3:a∈H⇔[a]_H=H(子群H和H内的元素构造陪集，必然是H本身)

a∈H，H={e,…a,…,h,…}

[a]_H={a*e,…,a*H,…}，由于群的封闭性，那么[a]_H⊆H。

∀ b∈H，a∈H可以推出a^-1^*b∈H，可以代表任意h。那么a^-1^*(a^-1^*b)=b∈[a]_H ，说明H的元素都在陪集，H⊆[a]H.

可得H=[a]H

定义4: **[a]_H =[b]_H ⇔a^-1^ * b∈H(或b^-1^ *a∈H)**。

先假设两个[a]_H=[b]_H

[b]_H={b,…,b*h,…},[a]_H={a,…,a*h,…}。那么在[a]_H 必然有b=a*h。，a^-1^*b=h∈H。 [a]_H =[b]_H ⇒a^-1^ * b∈H(或b^-1^ *a∈H)

反推: 比较简单不多赘述**[a]_H =[b]_H ⇐ a^-1^ * b∈H(或b^-1^ *a∈H)**

举个例子:

[0]_3Z={0,0±3,…,0±3n}

[1]_3Z={1,1±3,…,1±3n}

[2]_3Z={2,2±3n,…,2±3n}

[3]_3Z={0,0±3n,…,±3n}

……

设[a]_3Z 和[b]_3Z ，那么很明显的当|b-a|的绝对值=3n即属于3Z的时候，[a]_3Z =[b]_3Z

接下来我们来利用上面的性质介绍

拉格朗日定理(Lagranges’s theorem)

群的划分

我们对定义4进行另一种解释，当一个a和b的逆进行运算时，类似于a于b的差值，当这个差值h∈H时，则[a]_H =[b]_H

我们引入一个专门的二元关系: $a≡b (mod H)⇔a^{-1}* b∈H(b^{-1}*a∈H)⇔[a]_H=[b]_H$ 。这里的a≡b (mod H)是一种二元关系，不是取模那种二元运算。

前置定理

划分: 如果 S 不是一个空集并且可以写成一系列互相之间不相交的子集的并，那么我们说这些子集构成了 S 的一个划分。

集合与等价关系:
一个集合如果存在一个等价关系，那么我一定有办法对集合做一个划分。

一个集合中的一钟划分对应一个等价关系

等价关系与等价类。
1. ✅ 等价关系（Equivalence Relation）

设 ( A ) 是一个集合。若二元关系$ ( \sim \subseteq A \times A )$ 满足以下三个性质，则称其为集合 ( A ) 上的等价关系：

自反性：对任意$ ( a \in A )$，有 $( a \sim a )$
对称性：若$ ( a \sim b )$，则 $( b \sim a )$
传递性：若 $( a \sim b )$ 且$ ( b \sim c )$，则$ ( a \sim c )$
1. 🎯 等价类（Equivalence Class）

设 $( \sim )$ 是集合 ( A ) 上的等价关系，任取$ ( a \in A )$，定义：

$[
[a] = { x \in A \mid x \sim a }
]$

该集合称为元素 ( a ) 的等价类。

所有等价类在集合 ( A ) 中构成一个不交且完备的划分（partition）：

$[
A = \bigsqcup_{a \in A} [a]
]$（这里不用太在意，稍微理解就行）

    3.  📌 陪集（Quotient Set）

将集合 ( A ) 按照等价关系 ( $\sim$ ) 分类后，得到的所有等价类组成一个新集合，称为陪集：

$[
A / {\sim} = { [a] \mid a \in A }
]$

每个元素是一个等价类，是原集合在该等价关系下的分类单位。

根据上面的定理我们很容易证明$a≡b (mod H)$是一个等价关系，陪集是一个等价类

证明
1. 自反性: $a≡a(mod H)$
2. 对称性:$a≡b(mod H)⇒a=bh,h∈H⇒ah^{-1}=b (h^{-1}∈H)⇒b≡a(mod H)$
3. 传递性: $a≡b(mod H),b≡c(mod H)⇒a=bh,b=ch_1,h,h_1∈H⇒a=chh_1,h*h_1∈H⇒a≡c(mod H)$
性质1：任意两个陪集之间存在双射，任意陪集[a]_H和子群H是等势的。(同一个子群所构造的陪集大小是相等的(元素的数量)，并且等于子群的大小)

拉格朗日定理

定理: G是有限群，H是任意子群，则|H|||G| (G任意子群的阶必然是G的阶的因子)。

证明:

设H构造的陪集为$[a_1]_H,…,[a_n]H$,它们是G的划分所有，$|G|=\sum{i=1}^{n}|[a_i]H|=\sum{i}^{n}|H|=n|H| $，并且我们显然就能知道这个n就是这个子群H能产生的陪集的个数。
示例
设群 $\mathbb{Z}_6 = {0, 1, 2, 3, 4, 5}$，其运算为加法模 $6$。这是一个有限阿贝尔群。

考虑其子群 $H = {0, 3}$，这个子群由 $3$ 生成，记作 $3\mathbb{Z}_6$。

构造集合 $\mathbb{Z}_6$ 关于 $H$ 的陪集如下：

$0 + H = {0, 3}$
$1 + H = {1, 4}$
$2 + H = {2, 5}$

由于 $\mathbb{Z}_6$ 是阿贝尔群，群的陪集构成一个划分：

$\mathbb{Z}_6 / H = { {0,3},\ {1,4},\ {2,5} }$

每个陪集包含 $2$ 个元素，共有 $3$ 个陪集。

由拉格朗日定理，若 $H \le G$，则 $|G| = [G : H] \cdot |H|$。

在本例中：
- $|G| = |\mathbb{Z}_6| = 6$
- $|H| = 2$
- $[\mathbb{Z}_6 : H] = 3$
满足 $6 = 3 \cdot 2$，符合拉格朗日定理。

商群

正规子群

定义: 设定N是群G的子群，如果对于$∀a∈G$，都有$aN=Na$，称为N为G的正规子群
1. 性质1正规子群的陪集运算规律:$[a]_N*[b]_N=[a*b]N，(a,b∈G)$ 这是一种陪集与陪集的运算
$(ah)(bh1)$ ,h,h1,h2∈N可以表示$[ab]N$中的任意元素
=$a*(hb)h1=ab(h2*h1)$显然成立。

注意这里的子群并不一定满足交换律，这个推导利用的是两个陪集之间的映射。

商群

引入，在前面的描述中我们可以定义一个集合$G/N={[a]_N|a∈G}$ ，这是一个由子群N的陪集组成的集合
前面讲述的性质1作为集合G/N元素之间的运算。$[a]_N*[b]_N=[ab]N$这里的’‘是群G的运算,a,b∈G

G/N是一个群:
1. 封闭性:$[a]_N*[b]_N=[ab]N$ ，ab∈G，显然满足结合律
2. 结合律:$[a]_N*([b]_N*[c]_N)=[abc]_N=([a]_N*[b]_N)*[c]_N$
3. 单位元:$N=[e]_N,N*[a]_N=[a]_N,N*[a]_N=[a]_N$，显然满足
4. 逆元:$[a]_N*[a^{-1}]_N=N,[a^{-1}]_N*[a]_N=N$
定义:像这样由正规子群N构成的群$(G/N,*)$称为模N下的商群。
[G:N]：商群G/N的阶
1. 定理1: G是有限群，N是G的正规子群。则$[G:N]=\frac{|G|}{|N|}$ —证明看拉格朗日定理
2. 定理2:G是有限群，N是G的正规子群，K是N的正规子群。则有$[G:K]=[G:N][N:K]$
  
  证明:$[G:K]=\frac{|G/||K|}{|N|/|K|}=\frac{[G:K]}{[N:K]} $
阿贝尔群的商群
1. 性质1: H是阿贝尔群G的子群，对于∀a∈G，有$aH=Ha=[a]_H$ —（这个定理反过来不一定成立）
  
  证明:
  
  $aH={ah|h∈H}={ha|h∈H}=[a]_H$
2. 性质2:阿贝尔群的子群都是正规子群
3. 性质2:阿贝尔群的子群都可以构造商群
4. 性质3:阿贝尔群构造的商群也是子群
例子
📘 商群 $\mathbb{Z}_{12} / \langle 3 \rangle$ 的例子（体现商群结构）

设群 $G = \mathbb{Z}_{12}$，即模 $12$ 下的整数加法群：

$$
G = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
$$

这是一个阿贝尔群。

取 $H = \langle 3 \rangle = {0, 3, 6, 9}$，是 $G$ 的一个子群。

由于 $G$ 是阿贝尔群，所有子群都是正规子群，因此 $H \trianglelefteq G$。

构造商群 $G/H$，即 $G$ 关于 $H$ 的陪集集合：
- $[0] = {0, 3, 6, 9}$
- $[1] = {1, 4, 7, 10}$
- $[2] = {2, 5, 8, 11}$
所以：

$$
\mathbb{Z}_{12} / \langle 3 \rangle = { [0], [1], [2] }
$$

我们来定义商群上的加法：

$$
[a] + [b] = [a + b]
$$

比如：
- $[1] + [1] = [2]$
- $[2] + [2] = [4] = [1]$（因为 $4 \in [1]$）
- $[1] + [2] = [3] = [0]$（因为 $3 \in H$）
我们可以列出这个商群的加法运算表：

$+$ $[0]$ $[1]$ $[2]$

$[0]$ $[0]$ $[1]$ $[2]$

$[1]$ $[1]$ $[2]$ $[0]$

$[2]$ $[2]$ $[0]$ $[1]$

这正是 $\mathbb{Z}_3$ 的加法表！

$+$	$[0]$	$[1]$	$[2]$
$[0]$	$[0]$	$[1]$	$[2]$
$[1]$	$[1]$	$[2]$	$[0]$
$[2]$	$[2]$	$[0]$	$[1]$

群的同态与同构

群论中的同态和同构来描述两个群之间的相似关系。

从中文上粗略看，同构好像指相同结构，同态好像不好说。

先上结论，从相似关系的程度来看：相同＞同构＞同态，即同态要求比同构更宽松，同构是一种特殊的同态。

单射满射双射

单射（Injective）

设有两个集合 $A$ 和 $B$，一个函数 $f: A \to B$ 被称为单射，如果：

不同的元素在 $A$ 中映射到不同的元素在 $B$ 中。

也就是说，如果 $f(a_1) = f(a_2)$，那么必有 $a_1 = a_2$。

换句话说，函数 $f$ 在定义域中不会“合并”两个不同的输入。

数学表达式：
$ \forall a_1, a_2 \in A, ; f(a_1) = f(a_2) \Rightarrow a_1 = a_2 $

满射（Surjective）

一个函数 $f: A \to B$ 是满射，如果：

对于 $B$ 中的每一个元素 $b$，都至少存在一个 $a \in A$，使得 $f(a) = b$。

也就是说，$f$ 的像集（输出）覆盖了整个集合 $B$。

数学表达式：
$ \forall b \in B, ; \exists a \in A \text{ 使得 } f(a) = b $

双射（Bijective）

一个函数 $f: A \to B$ 是双射，如果它既是单射又是满射。

也就是说，$f$ 是一一对应的：每个 $A$ 中的元素有唯一的 $B$ 中的对应元素，且每个 $B$ 中的元素也有唯一的 $A$ 中的前像。

数学表达式：
$ \forall b \in B, ; \exists! a \in A \text{ 使得 } f(a) = b $

群同态(Group homomorphism)

定义:设群$(G,)$和群$(G’,\otimes )$ ,如果函数$f:G\longrightarrow G’$,对于∀a,b∈G都有$f(a,b)=f(a)\otimes f(b)$，则称f为$(G,)$到$(G,\otimes)$ 的群同态.

若$f:G\longrightarrow G’$,(后面简称f)，是单射，那么称f是单S同态
若f是满射，那么称f是满同态或上同态
若f是双射，那么称f是同构记作:$G\cong G’$

示例

群 A = (Z,+),a∈A，群B = {1, -1}，映射。

$f(a)=(-1)^a$

$f(a_1a_2)=(-1)^{a+a_2}$

明显，奇数映射到-1，偶数映射到1。他们满足同态映射。

同态像(homomorphism image)

定义:$Im f=f(G)={f(a)|a∈G}$

在群同态$f:G\longrightarrow G’$ 在元素G->G‘映射的落点可能只是G’的子集。像这样G’中能在G内找到原像的子集称为同态像。

同态核(homomorphism kernel)

定义: $Ker f={a∈G|f(a)=e’}$,e’是G’的单位元

核这个该概念关注的是定义域G内的元素。G内经f映射后等于G’内单位元的元素构成的集合称为同态核。

同态核的性质
1. 定义1: $f:G\longrightarrow G’$是群同态，则Ker f是正规子群。
证明: 设 $f: G \longrightarrow G’$ 是群同态。

定义核为：

$$
\ker f = { g \in G \mid f(g) = e_{G’} }
$$

我们要证明：$\ker f \trianglelefteq G$，即它是 $G$ 的正规子群。

证明：
1. $\ker f \neq \emptyset$，因为 $f(e_G) = e_{G’}$，所以 $e_G \in \ker f$。
2. 若 $a, b \in \ker f$，则：
$$
f(ab^{-1}) = f(a)f(b)^{-1} = e_{G’} e_{G’}^{-1} = e_{G’} \Rightarrow ab^{-1} \in \ker f
$$

所以 $\ker f \leq G$。
1. 对任意 $g \in G,; k \in \ker f$，我们有：
$$
f(gkg^{-1}) = f(g)f(k)f(g)^{-1} = f(g)e_{G’}f(g)^{-1} = f(g)f(g)^{-1} = e_{G’} \Rightarrow gkg^{-1} \in \ker f
$$

因此，$\ker f$ 对共轭封闭，是正规子群：

$$
\ker f \trianglelefteq G
$$
1. **定义2: 。$f:G \longrightarrow G’有f是单射\Leftrightarrow Ker f={e}$**l
  
  证明:$假设f不是单射，\exists a,b∈G，a≠,有f(a)=f(b).定理3，a\equiv b(mod Ker f)。
  所以,b^{-1}∈Ker f,b^{-1}*a≠e,与核里只有e矛盾$
2. 定义3$f:G\longrightarrow G’ $是群同态，∀ a,b∈G，有$f(a)=f(b)\Longleftrightarrow a\equiv b (mod Ker f)$
  
  证明:$f(a)=f(b)\Longleftrightarrow f^{-1}(b)\otimes f(a)=f^{-1}(b)\otimes f(b)=e’$
  - f是单一同态$\Longleftrightarrow$ Ker f={e}(同态核只要单位元)
  - f是满同态$\Longleftrightarrow$ Im f=G’(同态像是G其本身)

群同态的示例

嵌入映射(inclusion map)
- 定义:是数学中的一个基本概念，也称为包含映射。它是一种特殊的映射，用于描述一个集合如何嵌入到另一个集合中。
  
  设群$(G,*)，H\subseteq G$ 定义映射f为$f:H\longrightarrow G$
  
  显然有$a∈H，f(a)=a$
  
  证明:$\forall a,b∈H \ f(ab)=ab=f(a)*f(b)$
  
  所以子群到群的嵌入映射是群同态，这个群同态还有个特点是原像与像之间是一对一的。显然这是一个单射，这种群同态叫单一同态
自然映射(natural map)
- 定义：集合A上的等价关系R到商集A/R的映射
  
  设群$(G,*)，N\subseteq G$ 定义映射f为$f:G\longrightarrow G/N$
  显然有$a∈G，f(a)=[a]_N$。这里表示的是群G上的元素a到它的商群G/N上的映射
  
  证明:$\forall a,b∈G \ f(a,b)=[ab]_N=[a]_N[b]_N=f(a)*f(b)$
  
  显然这是一个群同态，在这个群同态中N是商群的单位元。那么自然映射构成的群的同态核就N，也就是商群的单位元。这个群同态因为每个陪集都有与之对应的原像(代表元)，所以它是个满射，这种群同态称为满同态。
m次方映射(n-power map)
- 定义:(不像上面有上面专门的概念我们这里给个数学定义)G是一个集合。$G’={f(a)|a∈G，f(a)=a^m}$ 这里的次方是指的进行m次运算。
  
  定义阿贝尔群$(G,*)$ ,定义映射f为$f:G \longrightarrow G^m$ 。这是一个群同态，在这个群同态中$Im f=G^m$ $Ker f=G{m}$(G^m^和G{m}是什么见前面群基础-子群-子群的构造)
  
  证明: $\forall a,b∈G\f(ab)=(ab)^m=a^m*b^m=f(a)*f(b)$
  
  例:
  
  $f: Z^*_p \longrightarrow Z^*_p ,a\longrightarrow a^2$
  
  那么在这个群同态中:$Im f=(Z^*_p)^2 ,Ker f=Z^*_p{2}={1,p-1} $

群同态的性质

性质1:群同态的单位元对应单位元。设e’是G‘的单位元。那么$f:G\longrightarrow G’$就有e’=f(e)。

证明:$f(ae)=f(a)f(e)=f(a)$，所以f(e)是单位元
性质2: 逆元对应逆元:$f(a^{-1})=f(a)^{-1} ,\forall a∈G $

证明:$f(a)f(a^{-1})=f(aa^{-1}=f(e))$
性质3: $H\subseteq G \Longrightarrow f(H)∈G’$ H是原群G的子群，那么f(H)也是同态映射后G‘的子群

证明:$\forall a,b∈H，f(a),f(b)∈f(H),则f(a)\otimes f(b)^{-1}=f(a) \otimes f(b^{-1})=f(ab^{-1})\因为ab^{-1}∈H，那么f(a*b^{-1})∈f(H)$

扩展:同态像$Im f$ 是G’ 的子群
性质4:$H’\subseteq G’\Longrightarrow f^{-1}(H’)∈G$ 。如果H’是同态映射后的群G‘的子群，那么f^-1^(H’)是原群G的子群
证明：

设 $( f: G \to G’ ) $是群同态，且 $( H’ \leq G’ )$，我们要证明$ \ f^{-1}(H’) \leq G )$。

记：

$$
f^{-1}(H’) = { g \in G \mid f(g) \in H’ }
$$

我们验证$ ( f^{-1}(H’) )$ 是否满足子群的三个条件：
1. 非空性：
由于 $( H’ \leq G’ )$，所以单位元 $( e_{G’} \in H’ )$。

又因为 ( f ) 是群同态，$( f(e_G) = e_{G’} \in H’ )$，所以 $（e_G \in f^{-1}(H’) )$，因此$ ( f^{-1}(H’) \neq \emptyset )$。
1. 封闭性：
任取$ ( a, b \in f^{-1}(H’) )$，则有：

$$
f(a), f(b) \in H’ \Rightarrow f(a)f(b) \in H’ \quad (\text{因为 } H’ \leq G’)
$$

由于 ( f ) 是同态，有：

$$
f(ab) = f(a)f(b) \in H’ \Rightarrow ab \in f^{-1}(H’)
$$
1. 逆元封闭性：
任取 $( a \in f^{-1}(H’) )$，则 $( f(a) \in H’ )$，而 ( H’ ) 是子群，所以：

$$
f(a)^{-1} \in H’ \quad \text{且} \quad f(a^{-1}) = f(a)^{-1} \in H’ \Rightarrow a^{-1} \in f^{-1}(H’)
$$

综上，$( f^{-1}(H’) )$ 满足子群判别法的三条性质，因此：

$$
f^{-1}(H’) \leq G
$$

推论:H’={e’}。那么可以得到同态核是G的子群
性质5: $f(a^m)=f(a)^m,\forall a∈G，\forall m∈Z$。比较简单，证明略了。

群同态的复合

定义:$f$是群$(G,\oplus)$ 到$(G’,\oplus)$ 的群同态，$’f$是$(G’,\oplus)$到$(G’’,\otimes)$ 的群同态，则$f$和$f’$ 的复合表示为:
$$
f’\circ f:G\longrightarrow G’’
$$
这也是群同态。

那么这两个群同态的复合就是一个从G到G’’的群同态。

证明:

$\forall a,b∈G，有f’\circ f(a*b)=f’\circ f(a)\otimes f’\circ f(b)$

群同构

定义:群同构是满足双射(单射和满射)的群同态。

定义G与G‘同构，记作$G\cong G’$ 。G与G之间的同构称为自同。同构的逆映射也是同构

群同构的意义:两个群的元素是一一对应，且运算规律得到保持，即使经过映射，群的所有结构特性得到保留。一堆同构的群只需要研究一个群的性质就行了。

引理1:设映射 $$f : G \to G’$$ 是群同态,同态核 $$Ker(f) = N$$，如果 $$H$$ 是 $$G$$ 的子群，则有 $$f^{-1}(f(H)) = HN$$。

证明:

任取元素 $$h \in H, n \in N$$，$$f(h * n) = f(h) \cdot f(n) = f(h)$$（同态核里的元素映射到 $$G’$$ 是单位元）故 $$f(HN) \subseteq f(H)$$。即：$$HN \subseteq f^{-1}(f(H))$$。对于任意 $$x \in f^{-1}(f(H))$$，有 $$f(x) \in f(H)$$。故存在 $$h$$ 使得 $$f(x) = f(h)$$。故 $$f(h^{-1} * x) = f(h^{-1}) \cdot f(x) = f(h^{-1}) \cdot f(h) = e’$$ 故 $$h^{-1}x \in N$$。$$x = hh^{-1}x \in HN$$ 即：$$f^{-1}(f(H)) \subseteq HN$$。 $$HN = f^{-1}(f(H))$$。

特别地，当 $$N \subseteq H$$ 时， $$HN = H$$（考虑陪集的性质），故 $$f^{-1}(f(H)) = H$$。

第一同构定理:(基本同态定理)

第一同构定理：(基本同态定理) 设 $f$ 是群 $G$ 到群 $G’$ 的群同态，两个群定义的运算为 $$、$\cdot$。同态核为 $K$，同态像为 $I$，则 $G/K \cong I$，这个群同构是把商群$$里的陪集$*$映射成代表元的像，设映射为 $\rho$，即: $[ \rho(aK) = f(a). ]$

证明: - (单射) :

$\forall a, b \in G$，若 $aK = bK$，由于 $\rho(aK) = f(a)$，则 $f(a) = f(b)$。

若 $aK \neq bK$，由陪集知识可知，$a \nsim b$，则 $b^{-1}a \notin K$（因为 $K$ 是 $G$ 的正规子群$*$）。

故 $f(b^{-1}a) = f(b)^{-1} \cdot f(a) \neq e’$（$e’$ 是群 $G’$ 的单位元），故 $f(a) \neq f(b)$。 - (满射) $\forall f(a) \in I$，都有对应的原像 $aK$，故是满射。

(群同态) $ [ \rho(aK * bK) = \rho(abK) = f(ab) = f(a) \cdot f(b) = \rho(aK) \cdot \rho(bK), ] $ 得证。 $\rho’ : G/K \to G’$ 是单一同态。

第二同构定理

第二同构定理：设 $f: G \to G’$ 是群的满同态，设同态核为 $N$。若 $H$ 是 $G$ 的包含 $N$ 的正规子群，记 $H’ = f(H)$，则有 $ [ G/H \cong G’/H’. ] $

证明：

**构造同态 $\psi$**：定义 $\psi: G \to G’/H’$，对 $\forall g \in G$，$\psi(g) = f(g)H’$（$f(g) \in G’$）。

 **满同态**：任取 $f(g)H' \in G'/H'$，其原像为 $g \in G$，故 $\psi$ 满。

 2. **计算核 $\text{Ker}(\psi)$**：     $[   \text{Ker}(\psi) = \{ g \in G \mid f(g)H' = H' \} = \{ g \in G \mid f(g) \in H' \} = f^{-1}(H').   ]  $   因 $H' = f(H)$ 且 $N \subseteq H$，由引理 $f^{-1}(f(H)) = HN = H$（$N \subseteq H$ 时 $HN = H$），

 故：    $ [   \text{Ker}(\psi) = f^{-1}(f(H)) = H.   ]$  

 ‘

 3. **应用第一同构定理**：     由第一同构定理，满同态 $\psi$ 诱导同构：    $ [   G/\text{Ker}(\psi) \cong \text{Im}(\psi) \implies G/H \cong G'/H' \quad (\text{因 } \text{Im}(\psi) = G'/H').   ]   $

 4. **推论**：   对自然同态 $\pi: G \to G/N$，若 $H \supseteq N$，则：   \[ (G/N)/(H/N) \cong G/H, \]   且 $H/N \triangleleft G/N \iff H \triangleleft G$（正规子群的商群对应性）。 

 5. **说明**：   - 第二同构定理通过构造满同态，利用核的性质（结合 $N \subseteq H$ 时 $f^{-1}(f(H)) = H$），将商群同构转化为第一同构定理的应用。   - 推论揭示了商群中正规子群的“提升”性质，是群论中分析子群与商群结构的关键工具。

第三同构定理

第三同构定理 **: 设 $H$ 是群 $G$ 的子群，$N$ 是群 $G$ 的正规子群，则 $H \cap N$ 是 $H$ 的正规子群，且 $H/(H \cap N) \cong HN/N$。 **

**证明: **

正规子群

$H \cap N$ 是 $G$ 的子群(子群的交是子群,也就是群),且 $H \cap N$ 是 $H$ 的非空子集(有单位元且 $H \cap N \subseteq H$ )。

故 $H \cap N$ 是 $H$ 的子群。

设群 $D = H \cap N$，

即证:$\forall h \in H, hD = Dh$。

对于∀$d_1 \in D$ ，都能找到 $d_2 \in D$ 满足 $hd_1 = d_2h$。 $hd_1h^{-1} = d_2 \in D$，

即满足 $hd_1h^{-1} \in H$ 且 $hd_1h^{-1} \in N$。

因为 $h, h^{-1} \in H, d_1 \in D \subseteq H, hd_1h^{-1} \in H$ (由于群的封闭性)。

至于 $hd_1h^{-1} \in N$,即:$hd_1 \in Nh = hN$ ($N$ 是群 $G$ 的正规子群)

，即:$d_1 \in N$ 。

$N$ 是群 $HN$ 的正规子群。

首先，我们知道 $HN$ 是群 $G$ 的子群。因为 $HN = NH$。

因为 $\forall h \in H, hN = Nh$。群 $N \subseteq HN$ (注:$N = eN$),加上它本身是群，故 $N$ 是 $HN$ 的子群。正规的说明同上，$N$ 是 $G$ 的正规子群，$\forall a \in HN \subseteq G, aN = Na$ 。

同构

构造 $\eta: H \to HN/N$,其中 $\forall h \in H, \eta(h) = hN$.(将群 $H$ 里的元素 $h$ 映射到商群 $HN/N$ 里)。

这是一个满同态。

对于每个 $hN$,都能在群 $H$ 里找到原像。

且 $Ker(\eta) = {h \in H|hN = N}$(同态核里的元素 $h$ 就是单位元) $= N \cap H$($h \in H$,且 $hN = N$,即 $h \in N$) 由同态基本定理， $H/(H \cap N)(H/ker(\eta)) \cong HN/N(\eta(H))$

群的结构

这一章我们主要将循环群，这是在密码学中一个很重要的概念。前面的同态和同构可能比较难理解可以只大概看一下，但是还是需要认真的看。

一种构造子群的方法：设G是群，$a∈G，则={a^z|z∈Z}$是由a生成的G的子群。

证明:$\forall a^i,a^j∈则a^i*(a^j)^{-1}=a^{i-j}∈$。

循环群

循环群的定义

定义: 设$G$是群，$g∈G$,如果$G=$，则称$G$是循环群，$g$表示循环群$G$的生成元。

示例:

整数加法群:$Z={z|z∈Z}={z*1|z∈Z}=<1>=<-1>$ -1和1是循环群Z的生成元—无限循环群

$Z^*_5$乘法循环群:
$Z^*_5={1,2,3,4}$ =<2>=<3>—-$2^1=2,2^3=3，2^4=1。3^2=4,3^3=2,3^4=1$—有限循环群

定理1: 任意循环群都是阿贝尔群

证明:$\forall a,v∈,设a=g^r,b=g^k，则ab=g^{r+k}=ba$
定理2:循环群的子群一定是循环群

证明: 证明设循环群 $G$，生成元为 $g$，群阶 $|G| = n$，

因为循环群 $G$ 中的任意一个元素都可以表达为生成元的幂的形式，故而，若 $H$ 为循环群 $G$ 的一个子群，则必然可写为

$ [ {g^{k_1}, g^{k_2}, \ldots, g^{k_m}}, \quad 1 < k_1 < k_2 < \ldots < k_m \leq n ] $

并引入$ [ d = \min{k_1, k_2, \ldots, k_m} ]$

因为 $G$ 是一个有限群，结合前要知识1知道，$G$ 中的任一元素的阶都存在，即任一元素都可以形成一个循环子群。故而对于元素 $g^d$，必然可以形成循环子群 $\langle g^d \rangle$。
定理3:设$G$是循环群,$H$是其子群，则商群$G/H$是循环群

证明
（循环群是阿贝尔群，而阿贝尔群的子群都是正规子群，所以 $H$ 是正规子群，它可以构成商群）

设 $G = \langle g \rangle$，则 $G/H = \langle [g]_H \rangle$。这是因为，

对于 $\forall [g^k]_H \in G/H$，有

$[
[g^k]_H = [g * \cdots * g]_H = [g]_H * \cdots * [g]_H = ([g]_H)^k
]$

所以，$\forall [g^k]_H$ 都是由 $[g]_H$ 生成。故而，$[g]_H$ 是 $G/H$ 的生成元。

元素的阶

定义: 设$G$是群，$a∈G$，如果n是满足$a^n=e$的最小的正整数，则称n是元素a的阶。
性质1**:$G$是群，元素a的阶是$n(a^n=e)$，则$\forall m∈Z$，有$n|m\Longleftrightarrow a^m=e$。**

这个是很显然的，就不证明了
性质2:有限循环群的阶是n，则生成元的阶也是n。

显然生成元生成不重复的元素最多也只有n个。
性质3:正整数$d|n$，n阶有限循环群恰有一个d阶的子群。

证明:(存在性):d|n,有$g^{n/d}$ 的阶是d。则$<g^{n/d}>$的阶是d。故而存在阶是d的子群$<g^{n/d}>$

（唯一性）反证法:假设存在另一个d阶的循环子群$<g^k>$，则$(g^k)^d=e$，所以n|kd，有$\frac{n}{d}|k $ 。所以,$g^{k}∈$

所以，$g^k∈<g^{\frac {n}{d} }>$,有$<g^k>$是$<g^{\frac {n}{d}}>$ ，因为二者阶都是d，所以他们是同一个循环群

例：循环群G的阶是15，15的正因子是1，3，5，15，所以G一个有4个子群。他们的阶分别是1，3，5，15。
性质4: n阶有限循环群，$\forall ∈Z$，有$g^k$的阶是$\frac {n}{gcd(n,k)}$ 。

证明:假设$g^k$的阶是m,则$g^{km}=e$，有$n|km$

于是,$km=lcm(n,k)=\frac {nk}{gccd(n,k)}$

所以，$m=\frac {n}{gcd(n,k)}$
性质5:n阶有限循环群有$\phi (n)$(欧拉函数)个生成元

根据上述的性质$order(g^k)(表示阶)=\frac {n}{gcd(n,k)}$ 。当gcd(n,k)=1时，$g^k$的阶为n，此时$g^k$ 是生成元
性质6:G是有限群，元素a的阶乘是|G|的因子。

$$是G的子群，根据拉格朗日定理，有$||||G|$

因为生成元a的阶等于的阶。所以，a的阶是|G|的因子

性质7: 素数阶的群必然是(有限)循环群。

证明：设 $G$ 是群，且 $|G| = p$，$p$ 是素数。

设 $a \in G$，且 $a \neq e$，$a$ 的阶是 $k$（$a^k = e$）。根据性质6，$k \mid p$。

所以，$k = 1$ 或 $p$。因为 $a \neq e$，所以 $k = p$，即 $a$ 的阶是 $p$，有 $a$ 是生成元。所以，$G$ 是(有限)循环群(因为它有生成元)。

设 $k$ 是 $a$ 的阶元素的阶是群的阶的因子

循环群的同构

无限循环群的同构群
- 定理:设$<G,*>$为无限循环群，则$<G,*>\cong <Z,+>$
  
  证明:$|a| = \infty$，令 $f: \mathbb{Z} \to G$ 如下：$f(n) = a^n$，
  
  因为 $f(n + m) = a^{n + m} = a^n * a^m = f(n) * f(m)$，所以 $f$ 为同态；
  
  又因为 $f(n) = f(m) \Rightarrow a^n = a^m \Rightarrow a^{|n - m|} = e \Rightarrow |n - m| = 0 \Rightarrow n = m$，所以 $f$ 为 1 - 1，onto 易见，从而 $\langle G, * \rangle \cong \langle \mathbb{Z}, + \rangle$
有限循环群的同构群
- 定理:设 $\langle G, * \rangle$ 为有限循环群，则 $\langle G, * \rangle \cong \langle \mathbb{Z}_n, \oplus_n \rangle$
  
  证明
  
  $|a| = n > 0$，从而 $G = {a^0, a^1, \cdots, a^{n - 1}}$，令 $f: \mathbb{Z}_n \to G$ 如下：$f(i) = a^i$ ($i = 0, 1, \cdots, n - 1$)，由于 $f(i \oplus_n j) = a^{i \oplus_n j} = a^i * a^j = f(i) * f(j)$，故 $f$ 为同态。又由于 $f(i) = f(j) \Rightarrow a^i = a^j \Rightarrow a^{|i - j|} = e \Rightarrow n \mid |i - j| \Rightarrow i \equiv j \pmod{n} \Rightarrow i = j$，故 $f$ 为单射，$f$ 的满射性易见，因此 $\langle G, * \rangle \cong \langle \mathbb{Z}_n, \oplus_n \rangle$
根据上面两个定理，我们讨论循环群讨论与它同构的 <Z,+>和$\langle \mathbb{Z}_n, \oplus_n \rangle$
性质8:$G$是n阶有限循环群，d是n的正因子，G里的d阶乘元素一共有$\phi (d)$个

设 $G$ 是一个有限循环群，$|G| = n$，即 $G \cong \mathbb{Z}_n$。

我们知道 $\mathbb{Z}_n = {0, 1, \dots, n-1}$ 在加法模 $n$ 意义下构成一个循环群，生成元为与 $n$ 互素的元素。

记 $d \mid n$，我们要求 $\mathbb{Z}_n$ 中阶为 $d$ 的元素个数。

步骤 1：$\mathbb{Z}_n$ 中元素 $a$ 的阶为 $\dfrac{n}{\gcd(a, n)}$

令 $\text{ord}(a)$ 表示 $a$ 的阶，则：

$$
\text{ord}(a) = \frac{n}{\gcd(a, n)}
$$

所以，当且仅当 $\gcd(a, n) = \frac{n}{d}$ 时，$\text{ord}(a) = d$。

步骤 2：求出满足 $\gcd(a, n) = \frac{n}{d}$ 的 $a$ 的个数

设 $m = \dfrac{n}{d}$，我们要求：

$$
#{a \in \mathbb{Z}_n \mid \gcd(a, n) = m}
$$

令 $a = m k$，则 $a < n$，即 $k < d$，并且 $\gcd(mk, n) = m \iff \gcd(k, d) = 1$。

所以，$k$ 满足 $1 \leq k \leq d$ 且 $\gcd(k, d) = 1$，这样的 $k$ 有 $\varphi(d)$ 个。

结论：

$$
\text{$G$ 中阶为 $d$ 的元素个数} = \varphi(d)
$$

群的直积

给定两个群: $(S, \circ), (T, *)$，定义笛卡儿乘积 $S \times T$ 上的运算 $\otimes$ 如下：
$[
\langle s_1, t_1 \rangle \otimes \langle s_2, t_2 \rangle = \langle s_1 \circ s_2, t_1 * t_2 \rangle
]$
$(S \times T, \otimes)$ 是群
- 结合律：
  $单位元素：$$\langle 1_S, 1_T \rangle$
- 逆元素：$\langle s, t \rangle$ 的逆元素是 $\langle s^{-1}, t^{-1} \rangle$
  - (其中：$s, s^{-1} \in S, t, t^{-1} \in T$)

循环群的直积

$C_m \times C_n \cong C_{mn}$ 如果 $m$ 与 $n$ 互质。其中 $C_k$ 表示 $k$ 阶循环群。
- $\Leftarrow$ 若 $m$ 与 $n$ 互质，只需证明 $C_m \times C_n$ 含有阶为 $mn$ 的元素。
  - $(a, b)^{mn} = e$，其中 $a, b$ 分别是 $C_m$ 和 $C_n$ 的生成元素。
  - 若 $(a, b)^k = e$，$k$ 必是 $m, n$ 的公倍数，因 $m$ 与 $n$ 互质，故 $k$ 是 $mn$ 的倍数。所以，$(a, b)$ 的阶是 $mn$。
- $\Rightarrow$ 若 $C_m \times C_n \cong C_{mn}$，则 $C_m \times C_n$ 是循环群，设其生成元是 $(s, t)$，则 $(s, t)$ 的阶是 $mn$，若 $\gcd(m, n) = k > 1$，则 $(s, t)^{mn/k} = e$，这与 $(s, t)$ 的阶是 $mn$ 矛盾。
  - 注意：$s^m = e_1, t^n = e_2$

math

#math

一篇文章速通群论

http://example.com/2025/05/30/群论/

Author

fox

Posted on

May 30, 2025

Licensed under

LitCTF复现 Next