Rockfox的密码记录

JQCTFone-line-crypto

assert __import__('re').fullmatch(br'flag\{[!-z]{11}\}',flag:=os.getenvb(b'FLAG')) and [is_prime(int(flag.hex(),16)^^int(input('🌌 '))) for _ in range(7^7)]

这是题目源码。这道题侧重点在于利用is_Prime函数的特性。

from sage.misc.sageinspect import sage_getsource
print(sage_getsource(Integer.is_prime))

查看sage的这个函数

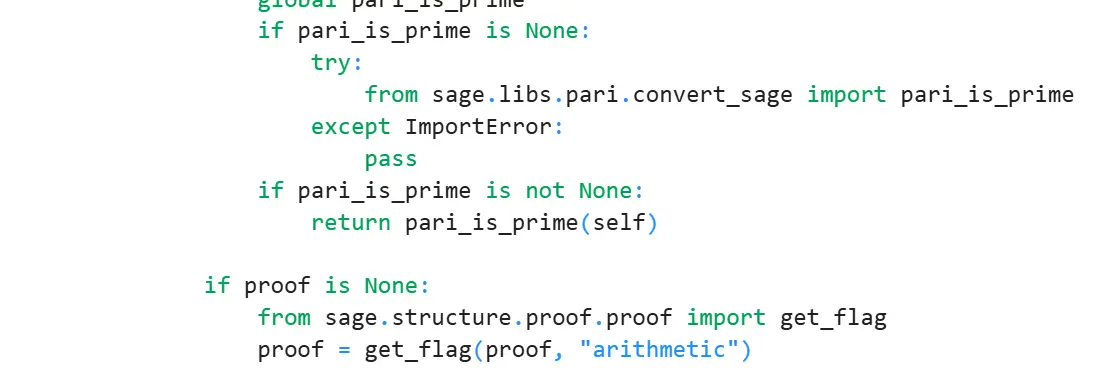
发现是基于pari_is_prime的，查看源码

long
BPSW_psp(GEN N)
{
  pari_sp av;
  if (typ(N) != t_INT) pari_err_TYPE("BPSW_psp",N);
  if (signe(N) <= 0) return 0;
  if (lgefint(N) == 3) return uisprime(uel(N,2));
  if (!mod2(N)) return 0;
#ifdef LONG_IS_64BIT
  /* 16294579238595022365 = 3*5*7*11*13*17*19*23*29*31*37*41*43*47*53
   *  7145393598349078859 = 59*61*67*71*73*79*83*89*97*101 */
  if (!iu_coprime(N, 16294579238595022365UL) ||
      !iu_coprime(N,  7145393598349078859UL)) return 0;
#else
  /* 4127218095 = 3*5*7*11*13*17*19*23*37
   * 3948078067 = 29*31*41*43*47*53
   * 4269855901 = 59*83*89*97*101
   * 1673450759 = 61*67*71*73*79 */
  if (!iu_coprime(N, 4127218095UL) ||
      !iu_coprime(N, 3948078067UL) ||
      !iu_coprime(N, 1673450759UL) ||
      !iu_coprime(N, 4269855901UL)) return 0;
#endif
  /* no prime divisor < 103 */
  av = avma;
  return gc_long(av, is2psp(N) && islucaspsp(N));
}

明显的，如果输入的N的有小于103的素因子，那么就不会进入真正的素数检测，而是直接return 0。

iu_coprime(N, 4127218095UL)是判断是否互质的函数。如果我们输入的N非常大，但是它没有小于103的素因子，那么它就会进入素数检测，因为N很大，那么这个函数所需要花费的时间明显是比有小于103的素因子的数N1花费的时间多，我们可以利用这一点做侧信道攻击。

利用时间不同我们可以判断输入的N^int(fllag)是否有小于103的素因子.

然后控制我们的输入，一种int(flag)<$2^{136}$ ,那么输入N=k*$2^{136}$ ,那么N^int(flag)=N+int(flag)。

再利用(flag+N)%p=0时，$flag\equiv -N mod p$ 。然后通过中国剩余定理就能做了

• 已知条件

prime∈{a|prime()<103}

$flag\equiv N mod p$ ,p∈{3,5,..101}。我们不知道具体的p和是多少，所以我们只能通过筛选和一定的爆破

• 优化方法

我们爆破的时候，可以遍历$r=Nmodp,r∈{1,p-1},N=k*2^{136}$，

一旦$r=Nmodp$与flag互为逆元 ,那么任意满足此条件的N满足(N+flag)%p=0

为了防止这个N是与其他不是p单仍是小于103的素数整除为0，我们需要测试多组满足此条件的N。如果连续多组仍然满足，则r=-flag mod p。注意因为N肯定是偶数所以我们排除掉2这个素数。然后因为最后一位肯定是’}’

那么

flag mod 256=ord(‘}‘)

• 解题代码

平台环境关了，这里做本地测试，为了节约时间，把$7^7$的循环次数改为$7 ^3$。

def task(input_num):
    flag = b"flag{$c4^Cr7=w!N}"
    flag_num = int(flag.hex(), 16)
    for _ in range(7**3):
        is_prime(flag_num^^input_num)
    return 1

import random
from math import prod
import time
primes_le_103 = [
    2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
    47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101
]

def task(input_num):
    flag = b"flag{$c4^Cr7=w!N}"
    flag_num = int(flag.hex(), 16)
    for _ in range(7**3):
        is_prime(flag_num^^input_num)
    return 1

def server_side_channel_oracle(input_num):
    st = time.time()
    a=task(input_num)
    et = time.time()
    return 0.002<(et-st)


def sample_mod_r_mod_p(r, p, bit_length = 32, start_bit = 136):
    assert p != 2, "p=2"
    while True:
        randnum = random.getrandbits(bit_length) << start_bit
        if randnum % p == r:
            yield randnum

def recover_flag(n_sample = 50):
    moduli = {}
    moduli[256] = ord("}")
    for p in primes_le_103[1:]:
        for k in range(p):
            count = 0
            good_k = True
            for input_num in sample_mod_r_mod_p(k, p):
                if not server_side_channel_oracle(input_num):
                    count += 1
                    if count == n_sample:
                        break
                else:
                    good_k = False
                    break
            if good_k:
                print(f"p: {p}, k: {k}")
                moduli[p] = (-k) % p
                break

    primes = [256] + primes_le_103[1:]
    remainders = [moduli[p] for p in primes]
    x = int(crt(remainders, primes))
    N = int(prod(primes))
    while True:
        hex_str = hex(x)[2:]
        if len(hex_str) % 2 != 0:
            hex_str = '0' + hex_str
        if b"flag" in bytes.fromhex(hex_str):
            return bytes.fromhex(hex_str).decode('utf-8')
        x += N

flag = recover_flag()
print("Recovered Flag:", flag)